The isometric projection of an object on a vertical plane of projection by placing the object in such a way that its three perpendicular edges make equal inclinations with the plane of projection.
Isometric Projection
Since the three perpendicular edges of an object are projected in the isometric projection at equal axonometric angles, the angles between those edges in the isometric projection will be at 120º. The lengths of the three perpendicular edges of an object in the isometric projection are foreshortened in the same proportion.
To understand the principles of isometric projection and to know the extent to which the edges are foreshortened.
A cube is placed with three of its perpendicular edges making equal inclinations with the vertical plane of projection and is projected on it. As shown in figure a.
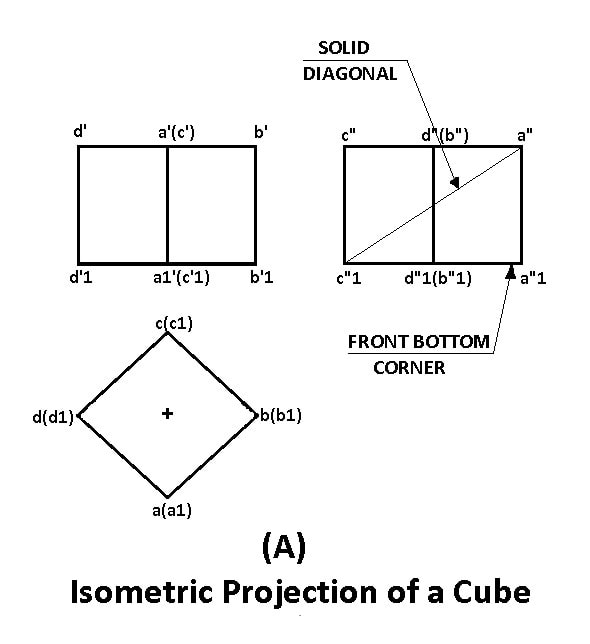
The projections of a cube when placed on HP such that two of its square faces making equal inclinations with the plane of projection.
Next, tilt the cube towards the observer such that it rests on the front bottom corner with the solid diagonal opposite to the corner in which it rests and passing through the top front corner, is perpendicular to the plane of projection.
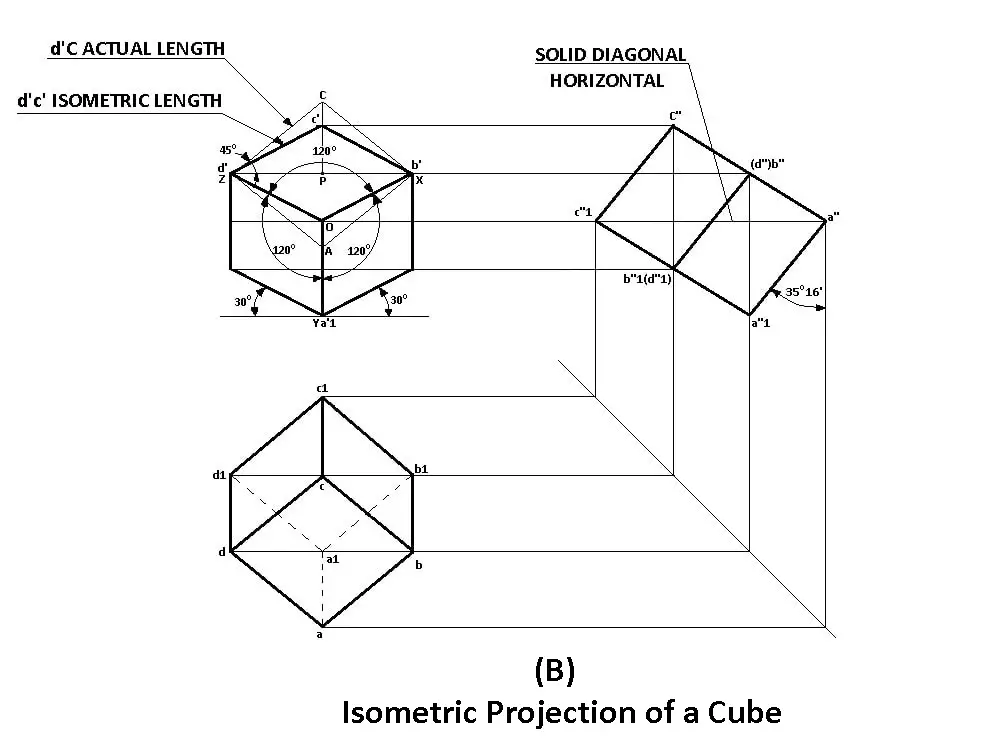
The Figure-B illustrates this position of the cube. As seen in the left view, the solid diagonal a “c1” is perpendicular to the plane of projection. In this position, the front and top views are projected. The three perpendicular edges AB, AD & AA1 will be equally inclined at an angle of 35° 16′ to the plane of projection.
But the projection of these edges, i.e., a’b’, a’d’ & a’a1′ are at an angle of 120º to each other and also they are foreshortened to the same length. The front view of the cube, therefore, represents its isometric projection.
Read also: Dimensions and Types of Dimensioning Systems
To Find The Length of The Edges in The Isometric Projection:
To find the extent to which the lengths of the edges are foreshortened.
Draw a square d’Ab’C od sides equal to the actual length of the edges of the cube with d’b’ as the common diagonal. d’C is the actual length of the edge, whereas corresponding edge d’c’ in the isometric projection is foreshortened. This foreshortened length is known as isometric length of the edge of the cube.
d’C is the actual length of the edge, whereas corresponding edge d’c’ in the isometric projection is foreshortened. This foreshortened length is known as the isometric length of the edge of the cube.
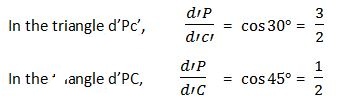
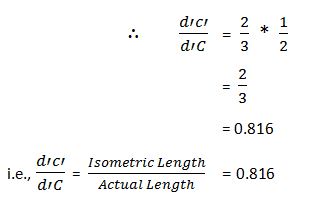
i.e., Isometric Length = 0.816 Actual Length. Thus in the isometric projection, the actual lengths of the objects are reduced in the ratio of 2:3. Or the isometric length is 0.816 of the actual length.
When an isometric projection is to be drawn, all the edges of the object parallel to the three isometric axes, have to be reduced to their corresponding isometric lengths which will be equal to 0.816 times their actual length.
Isometric Scale
In isometric projection, all edges of the object along the direction of three isometric axes are foreshortened to 0.816 times their exact lengths. To facilitate the easy and quick method of measurement of lengths of the various edges in their reduced sizes while drawing the isometric projection of the object, a special scale known as the isometric scale is constructed.

On this scale, the isometric lengths corresponding to the given actual lengths can be obtained directly. The isometric scale is constructed as follows:
Draw a horizontal line OA. THrough O draw OP and OQ at 30º & 45º to the horizontal respectively. On OQ mark the actual scale in mm. Draw verticals from each of the division points on the actual scale to cut OP at the corresponding divisions. The division points obtained on OP, called isometric scale, measure the distances reduced to isometric lengths.
Isometric View or Isometric Drawing
To draw the isometric projection of an object, every dimension of the object along the isometric axes, have to be reduced to the isometric scales.
This has two disadvantages:
- First, it is time-consuming and
- It is on such a drawing when required the distances between any two points along the isometric axes cannot be measured directly with the actual scale.
To overcome these difficulties, an object can be quickly represented in the isometric form using the actual scale instead of the isometric scale. Such a view will be precisely is of the same shape but larger than that drawn to the isometric scale.

The Figure-A shows a cube of 20mm sides drawn to the isometric scale.
The Figure-B shows the cube of the same dimensions drawn to the actual scale.
The view drawn to the exact scale is known as the Isometric View (Isometric Drawing). While that drawn using the isometric scale is known as as the Isometric Projection.
Isometric & Non-Isometric Lines
In the figure, the three perpendicular edges of the cube OX, OY, & OZ are foreshortened equally and are at equal inclinations of 120º to each other and are known as isometric axes. The lines drawn parallel to the isometric axes are known as Isometric Line.

Any other line which is not parallel to any of the isometric axes is known as Non-Isometric Line. The lines XY, YZ & ZX are called non-isometric lines.
Since these lines are not parallel to the isometric axes, they are not foreshortened in the same proportion as the isometric lines. Also, those horizontal edges of the object which are non-isometric must not be drawn at 30º. To draw the non-isometric lines, their ends should be located and then joined. The surface XYZ is an oblique surface in isometric.
Different Positions of Isometric Representation
An object in isometric projection may be shown in eight different positions as shown in the Figure. Anyone particular position may be selected so as to illustrate all the important details of the object clearly.

However, the object will be drawn in isometric with its longest measurement either vertical or horizontal. The position in figure-B is known as an isometric projection with axis reversed is drawn when the underneath surface of the object is to be shown.
That’s it. Thanks for reading if you have any questions about “Isometric Projection” ask in the comments I’ll respond to you. Share this post if it’s worth sharing.
If you like this article then please share it with your friends. And also you can download the free PDF file of this article by clicking below.
Subscribe to the newsletter to get notifications of our new posts. It’s Free.
You might like to explore more in our blog:
Plz enable the download option PDF of this
I updated the article with a PDF please check out, and thanks for reading.
Plz enable the PDF of this