Application of Bernoulli’s Equation: Assumptions, Equation, Principles

In this article, you will learn what is Bernoulli’s Equation and It’s Application, Working principle, Assumption, Equation, and Relation between Conversion of Energy and Bernoulli’s Equation.

Theory of Bernoulli’s Equation

Bernoulli’s theory, expressed by Daniel Bernoulli, it states that as the speed of a moving fluid is raises (liquid or gas), the pressure within the fluid drops. Even though Bernoulli cut the law, it was Leonhard Euler who assumed Bernoulli’s equation in its general form in 1752.

Bernoulli’s law says that “The total mechanical energy of the moving fluid that carries the gravitational potential energy of the elevation, the energy connected with the fluid pressure and the kinetic energy of the fluid motion is kept constant”.

This law theory can be derived from the principle of energy conservation.

Bernoulli’s Equation

The Bernoulli’s equation says that “for a completely incompressible fluid, moving in a continuous flow, the entire energy of a particle maintains the same, while the particles travel from one end to another”.

There is one assumption that “there are Friction Losses in Pipe”.

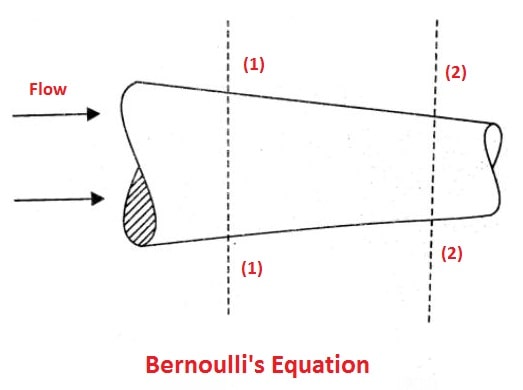
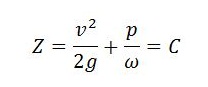
Bernoulli’s equation is one of the most essential and beneficial equations in fluid mechanics. It may be written,

According to Bernoulli’s equation

The energy in section 1 = energy in section 2

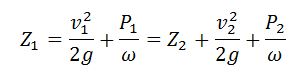
Relation Between Conservation of Energy and Bernoulli’s Equation

Conservation of energy is applied to fluid flow to produce Bernoulli’s equation. It is done is the result of the change in the kinetic energy of the fluid and the gravitational potential energy. Bernoulli’s equation can be modified based on the form of energy it contains. Other forms of energy include the distribution of thermal energy due to fluid viscosity.

Application of Bernoulli’s Equation

Following are the applications of Bernoulli’s equation:

1. Bernoulli’s equation is applied to all problems of incompressible fluid flow.
2. The Bernoulli’s equation can be applied to the following measuring devices such as Venturi meter, Nozzle meter, Orifice meter, Pitot tube and its applications to flow measurement from takes, within pipes as well as in open channels.
3. Bernoulli’s theory is used to study the unstable potential flow used in the theory of ocean surface waves and acoustics.
4. It is also employed for the estimation of parameters such as pressure and fluid speed.
5. Bernoulli’s principle can be applied in an aeroplane. For example, this theory explains why aeroplane wings are curved upward and the ships have to run away from each other as they pass.

Assumptions

The following are the assumptions made in the derivation of Bernoulli’s equation:

1. The fluid is ideal or perfect, that is viscosity is zero.
2. The flow is steady (The velocity of every liquid particle is uniform).
3. There is no energy loss while flowing.
4. The flow is incompressible.
5. The flow is Irrotational.
6. There is no external force, except the gravity force, is acting on the liquid.

Limitations

The following are the main limitation of Bernoulli’s equation:

1. The velocity of the fluid particle in the centre of a pipe is maximum and due to the friction, it gradually decreases towards the pipe walls. Thus while using Bernoulli’s equation, only the mean velocity of the liquid should be taken into account because the velocity of the liquid particles is not uniform. As per assumption, it is not practical.
2. There are always some external forces acting on the liquid, which affects the flow of friction. Thus while using Bernoulli’s equation all such external forces are neglected which has not happened in actual practice. If some energy is supplied to or extracted from the flow, the same should also take into account.
3. In turbulent flow, some kinetic energy is converted into heat energy and in viscous flow, some energy is lost due to shear forces. Thus while using Bernoulli’s equation all such losses should be neglected, which has not happened in actual practice.
4. If the fluid is flowing by a curved path, the energy due to centrifugal forces must also be taken into account.

---

That’s it

Thanks for reading the article on “Application of Bernoulli’s Equation”. If you like this let us know in the comments section and share with your friends.

Read Next:

1. Fluid: Properties of Fluids [Briefly Explained]
2. Mechanical Pressure Gauges: Types, Working, Applications, Advantages and More
3. What Are The Different Types of Manometers? Its Advantages and Disadvantages