Introduction to Conic Sections
Conic sections are mathematically defined as the curves formed by the locus of a point that moves a plant such that its distance from a fixed point is always in a constant ratio to its perpendicular distance from the fixed line.
These three types of curves sections are Ellipse, Parabola, and Hyperbola. The curves, Ellipse, Parabola, and Hyperbola are also obtained practically by cutting the curved surface of a cone in different ways.
The profiles of the cut-flat surface from these curves are hence called conic sections. The figure shows the different possible ways of cutting a cone.
Conic Sections

When a cone is cut by a plane perpendicular to the axis of the cone, the conic section will be a circle in Figure-A the plane-1 cuts the cone with its surface perpendicular to the axis of the cone so as to produce a circle as shown in Figure-B.
When a cone is cut by a plane making an angle with the axis, greater than the generators of the cone make with the axis and so as to cut both the end generators of the cone, the conic section will be an Ellipse. In Figure-A the plane-2 cuts the axis of the cone so as to produce an ellipse as shown in Figure-C.
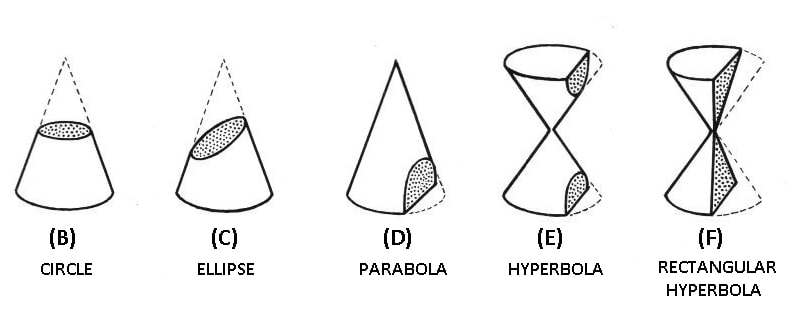
When a cone is cut by a plane parallel to one of the end generators of the cone, the conic section will be a parabola in Figure-A the plane-3 is parallel to the right end generator of the cone so as to produce a parabola as shown in Figure-D.
When a cone is cut by a plane making an angle with the axis smaller than generators make with the axis, the conic section will be a Hyperbola. In Figure-A the plane-4 cuts the axis of the cone so as to produce a hyperbola as shown in Figure-E.
When a cone is cut by a plane parallel to the axis of the cone the conic sections will be a Rectangular Hyperbola in Figur-A the plane-5 is parallel to the axis of the cone so as to produce a rectangular hyperbola as shown in Figure-F.
Read Also: Surface Finish & Surface Roughness with Indication & Symbols – Engg Drawing
Conic Sections Terminology:
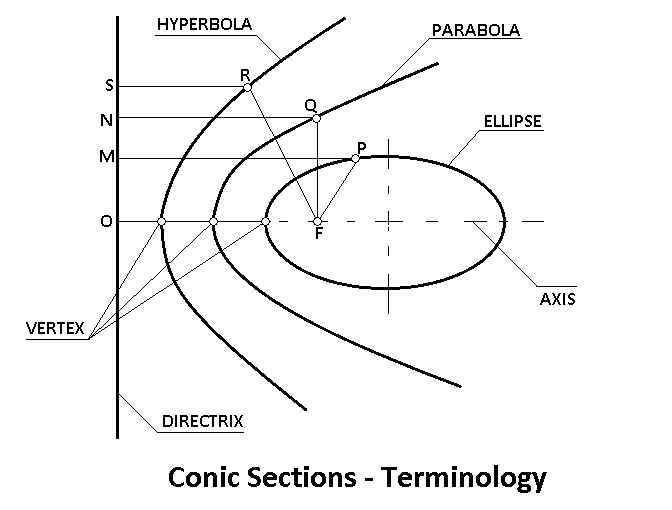
The fixed point is called Focus, the fixed line is called Directrix, and the ratio of the distance of the tracing point from the focus to its perpendicular distance from the directrix is called eccentricity.
A point at which the curves cut an axis is known as the vertex.
Definitions:
- Ellipse is the locus of a point P which moves such that the ratio of its distance from the fixed point F to its distance from a fixed line is a constant and is always less than 1.
- Parabola is the locus of a point Q which moves such that the ratio of its distance from the fixed point F to its distance from the fixed-line is a constant and is always equal to 1.
- Hyperbola is the locus of a point R which moves such that the ratio of its distance from the fixed point F to its distance from the fixed-line is a constant and is always greater than 1.
Ellipse
Applications: Ellipse is the most commonly used mathematical curve often employed in architectural and engineering constructions, Figure shows the few applications of the ellipse in engineering constructions.
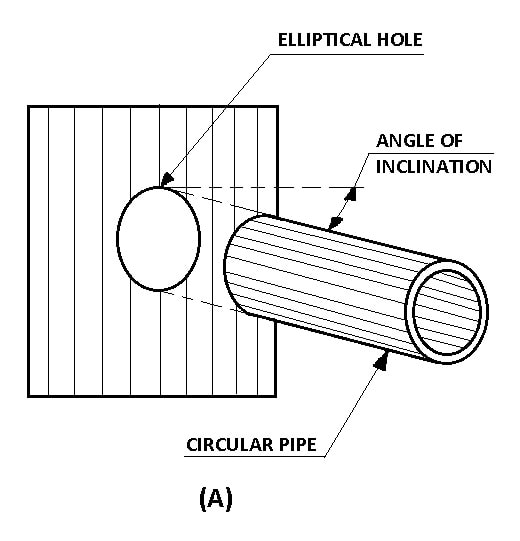
Whenever a cylindrical pipe is to be connected to a plane surface inclined to it, the profile of the end of the pipe which is connected to the plane surface and the shape of the hole in the plane surface will have to be ellipse as shown in Figure-A.
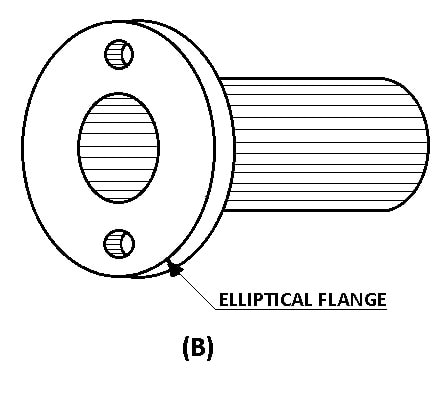
The flanges of pipes are generally designed to be elliptical as shown in Figure-B.
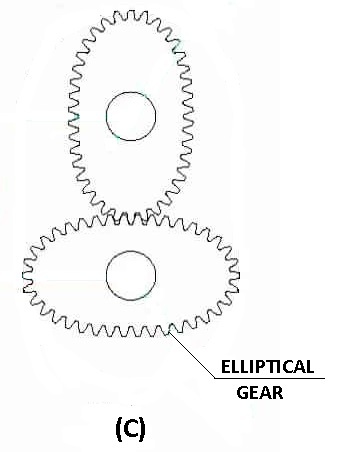
The elliptical gears shown in Figure-C are used to obtain varying speed rate in each revolution in packaging machines, textile equipment, flying shears, printing machines, etc.
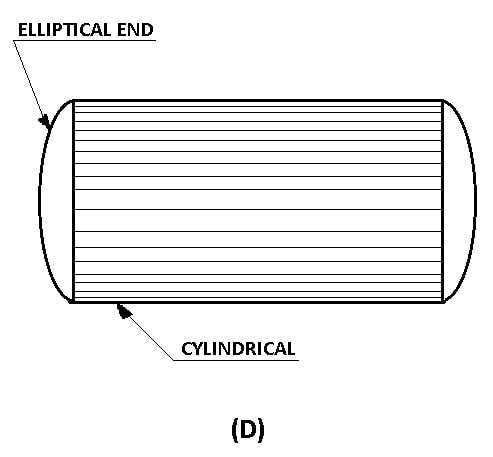
The ends of cylindrical tanks are made generally elliptical as shown in Figure-D.
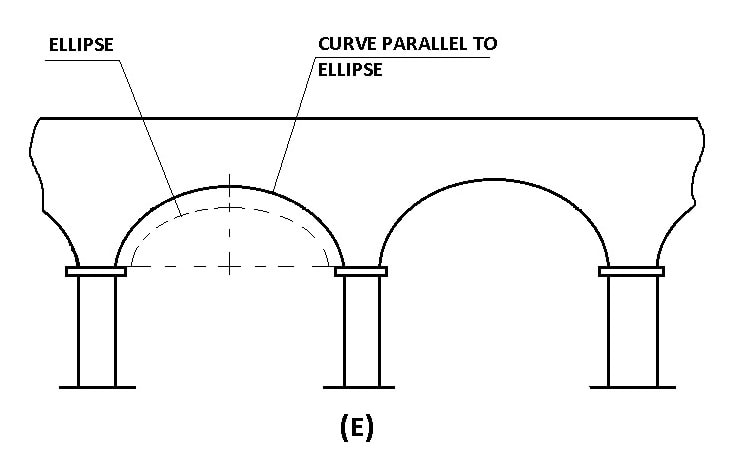
The arches of bridges will be generally of curves parallel to an ellipse as this gives greater vertical clearance near the abutments than the true ellipse as shown in Figure-E.
Definition and Terminology:
Ellipse is also defined as the locus of a point which moves such that the sum of its distances from the two fixed points is a constant which is equal to the length of the major axis.
F1 and F2 are two fixed points called foci. The line AB which passes through the foci with its end A and B lying in the curve is called a major axis. The line CD which bisects the axis having its ends C and flying on the curve is called minor axis.
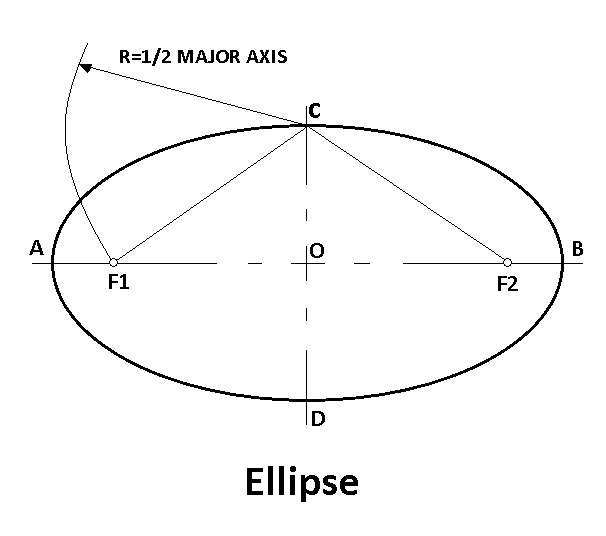
By using the above definition, when the major and minor axis is given, location and the distance between the foci can be found.
To find foci when Major nad Minor axis are given in Figure.
Since C is a point in the ellipse, the sum of its distances from F1 & F2 is equal to the major axis.
i.e., CF1+CF2=AB
Since C is a point on the minor axis,
CF1=CF2
∴CF1=CF2=(1/2) AB
When the major and minor axis are given the location of the foci are found as follows. Draw the major & minor axis. With C or D as centre and radius (1/2), AB cut AB at F1 & F2.
Read also: What is Isometric Projection? [Isometric View, Drawing and Representation]
Parabola
Applications: Parabola is widely used in engineering practice. Reflectors for parallel beams such as searchlights, headlamps of motor vehicles, etc, are in shape of a parabola. The light rays emanating from the incandescent filament fixed at the focus of a parabolic reflector are reflected from each point of the reflector parallel to each other as shown in the Figure-A.
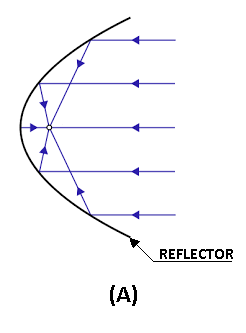
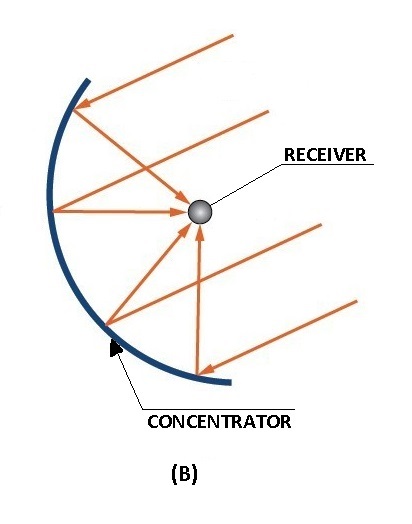
Similarly, all parallel rays cast onto a parabolic receiver are concentrated at the focus as shown in Figure-B. This property of parabolic receivers is used in solar concentrators.
The parabolic shape is also used in machine tool building. The cantilever type of arms and wall brackets which are subjected to heavy bending loads are frequently designed to the shape of a parabola as shown in the Figure-C.
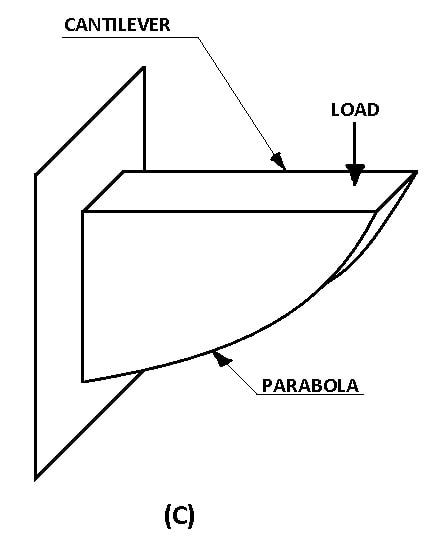
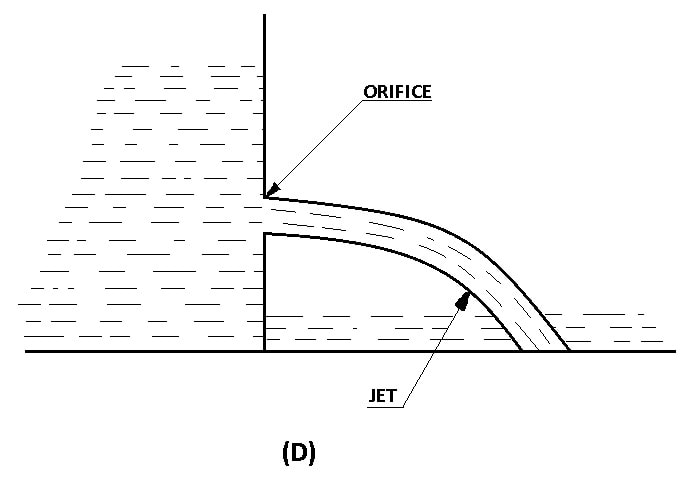
Such support of uniform strength offers the same resistance to bending. Parabolas are found in mechanics. The trajectory of a thrown object or missile is parabolic. The path of a jet of water issuing from a vertical orifice is parabolic as shown in Figure-D.
Hyperbola
Terminology:
Hyperbola is also defined as the curve generated by a point moving so that the difference between its distance from the two fixed points. F1 & F2 called foci is a constant, which is equal to the distance between A & B, the vertices of the hyperbola.
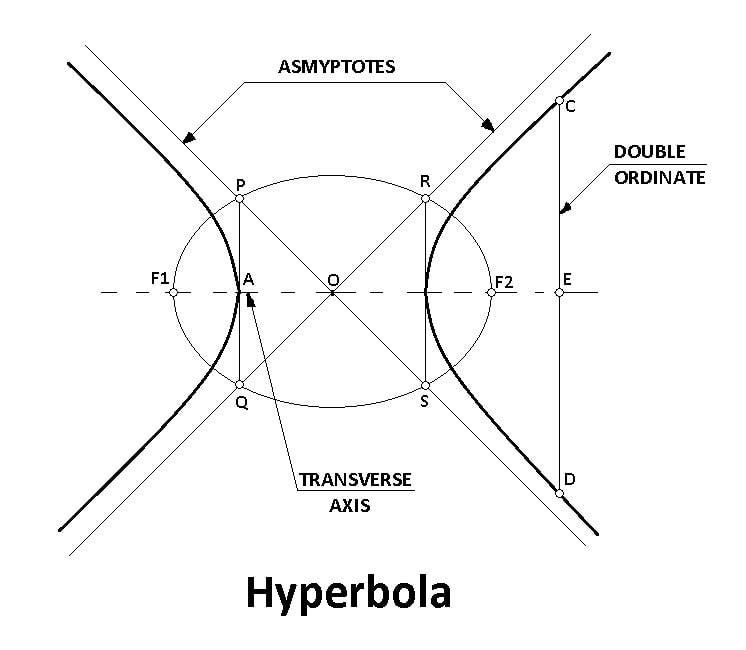
The distance between the two intersecting lines, called asymptotes PS & RO passing through the centre O, when produced approach nearer and nearer to the curves and will be tangential to the curves at infinity. When the asymptotes are at right angles, the curve is called rectangular or equilateral hyperbola.
Asymptotes are obtained as follows. With O as centre and radius, OF1 draw a circle. At A & B erect verticals to cut the circle at P, O, R & S. Connect PS & RO and produce them on either side.
That’s it, thanks for reading. If you have any questions about the “conic sections” ask in the comments I’ll respond to you. If you like this article please share it with your friends. Subscribe to our newsletter. It’s Free.
Download PDF of this article:
Read Next:
Very interesting can I have the PDF of it via email
Thanks for reading. I have sent the PDF file to your email.