In this post, you’ll learn what is Carnot Vapour Cycle its process and efficiency with p-v and t-s diagram.
Introduction to Carnot Vapour Cycle
In a vapour cycle, all the theory remains the same as thermodynamic cycle except the working substance, which is steam. The steam may be in any form, i.e. wet, dry or saturated or superheated.
A Carnot cycle steam as a working substance is represented on the p-v and T-s diagram in Figure.
Carnot Vapour Cycle P-V Diagram
Carnot Vapour Cycle T-S Diagram
Consider 1 kg of saturated water at pressure p1, and absolute temperature T1, as represented by point 1 in the figure.
Read also: Thermodynamic Cycle: Its Classification, Working, Terms Used in Thermodynamics and More.
Carnot Vapour Cycle Processes
The cycle is completed by the following four processes:
- 1-2 Process (Isothermal Expansion)
- 2-3 Process (Adiabatic Expansion)
- 3-4 Process (Isothermal Compression)
- 4-1 Process (Adiabatic Compression)
Read also: Carnot Cycle: Principle Processes, Efficiency with [P-v and T-s Diagram]
1. Process 1-2 (Isothermal Expansion)
- The water is isothermally converted into dry saturated steam, at a constant temperature (T1) and pressure (p1).
- Dry state of steam is expressed in point 2.
- It means that the temperature T2 (i.e., at point 2) and pressure p2 (i.e., at point 2) is equal to temperature T1 and pressure p2 respectively.
- This isothermal expansion is represented by curve 1-2 on p-v and T-s diagram in the figure.
- We know that the heat is absorbed by water during its conversion into dry steam is its latent heat (L1).
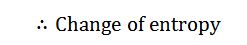
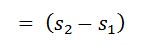
We also know that the area 12 ba in the T-s diagram represents the heat absorbed to some scale, during the isothermal expansion.
Heat absorbed during an isothermal expansion (area 12 ba)
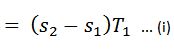
2. Process 2-3 (Adiabatic Expansion)
The dry steam now expands adiabatically. The pressure and temperature drop from p2 to p3 and T2 to T3. As no heat is supplied or rejected during this process, there is no change of entropy. The adiabatic expansion is represented by the curve 2-3 as shown in the figure.
Read also: Important Terms Used In Thermodynamics
3. Process 3-4 (Isothermal Compression)
- The wet steam is now isothermally compressed at constant temperature (T3) and pressure (p3).
- It means that the temperature T4 (i.e., at point 4) and pressure p4 (i.e., at point 4) is equal to the temperature T3 and pressure p3 respectively.
- This isothermal compression is represented by the curve 3-4 on p-v and T-s diagrams as shown in the figure.
We know that area 3-4 in the T-s diagram represents the heat rejected to some scale during the isothermal compression.
Heat rejected during isothermal compression (area 34 ba)
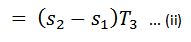
4. Process 4-1 (Adiabatic Compression)
- The wet steam at point D is finally compressed adiabatically, till it returns back to its original state (point 1).
- The pressure and temperature rise from p4 to p1 and T4 to T1 respectively.
- The adiabatic compression is represented by the curve 4-1 as shown in the figure.
- Since no heat is absorbed or rejected, therefore entropy remains constant. This completes the cycle.
We know that work done during the cycle
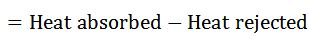
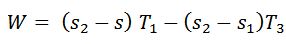
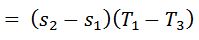
And the efficiency of the Carnot cycle,
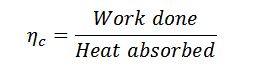
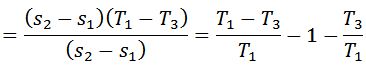
Notes:
- Since the heat absorbed is at the highest temperature and rejected at the lowest temperature, the Carnot cycle would give a maximum possible efficiency.
- In the above theory, we have taken the temperature at points 1, 2, 3 and 4 as T1, T2, T3 and T4 respectively in order to keep similarly between the Carnot cycle and other cycles. But some authors take it T1 (for points 1 and 2) and T2 (for points 3 and 4). In that case, they obtain the relation for efficiency as,
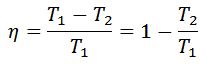
- It may be noted that it is impossible to make a steam engine working on the Carnot cycle.
- The simple reason for the same is that the isothermal expansion 1-2 will have to be carried out extremely slow to ensure that the steam is always at temperature T1.
- Thus, the isothermal compression 3-4 will have to be carried out extremely slow. But adiabatic expansion 2-3 and adiabatic compression 4-1 should be carried out as soon as possible in order to approach ideal adiabatic conditions.
- We know that sudden changes in engine speed are not possible in actual practice.
- In addition, it is very difficult to entirely eliminate friction between the various moving parts of the engine, and there are also heat losses due to conduction, radiation, etc.
- It is thus obvious, that it is impossible to realise Carnot’s engine is used as the ultimate standard of comparison of all steam engines.
That’s it, thanks for reading. If you have any questions about the “Carnot Vapour Cycle” tell us in the comments. If you like this article please share with your friends.
Read Next: